Identifying players who can break out in fantasy and DFS in Week 7.

• Calvin Ridley And Da’Lynn Polk stand out as candidates for super regression if their defenders can get the ball to them.

• With a new QB, Amari Cooper maybe we are in for a day of big positive regression. Judging by his routes and usage, he needs it.

• Unleash your benefits with a PFF+ subscription: Get full access to all of our seasonal fantasy tools, including weekly ratings, WR/CB Matchup Schedules, weekly forecasts, Launch and squat optimizer and much more. Register now!

Estimated reading time: 8 minutes

Fantasy and DFS enthusiasts, players and analysts often rely on a wide range of statistics and models to gain a competitive advantage. These range from basic scoring statistics to advanced metrics available in PFF 2.0 Premium Statistics And models such as Josh HermsmeyerBuy Low and WOPR (Weighted Opportunity Rating) model.

There is always room for new ideas and analysis to help bettors and fantasy managers improve their strategies. That’s why I developed a new metric that has several advantages over WOPR.

For the uninitiated, WOPR, calculated as (1.5 * Target Share) + (0.7 * Air Yards Share), is widely considered one of the most effective and predictable opportunity metrics in fantasy football.

In my approach, I used a predicted targets model along with a predicted air yards model to create advanced route-level receiving metrics. In this article I will draw on ideas from my Week 5 “Coach, I was open!” article and provide a projected WOPR that includes my variables “Proportion of Predicted Targets” and “Proportion of Predicted Air Yards” from Week 6..

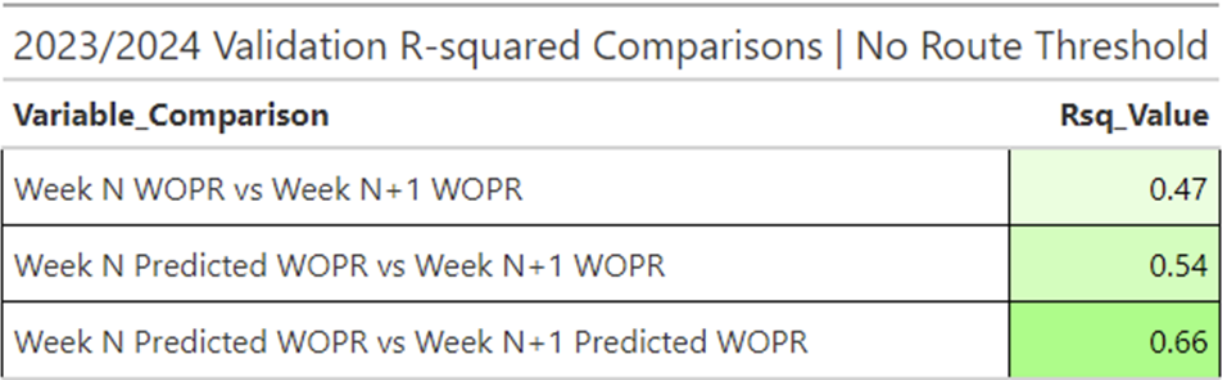
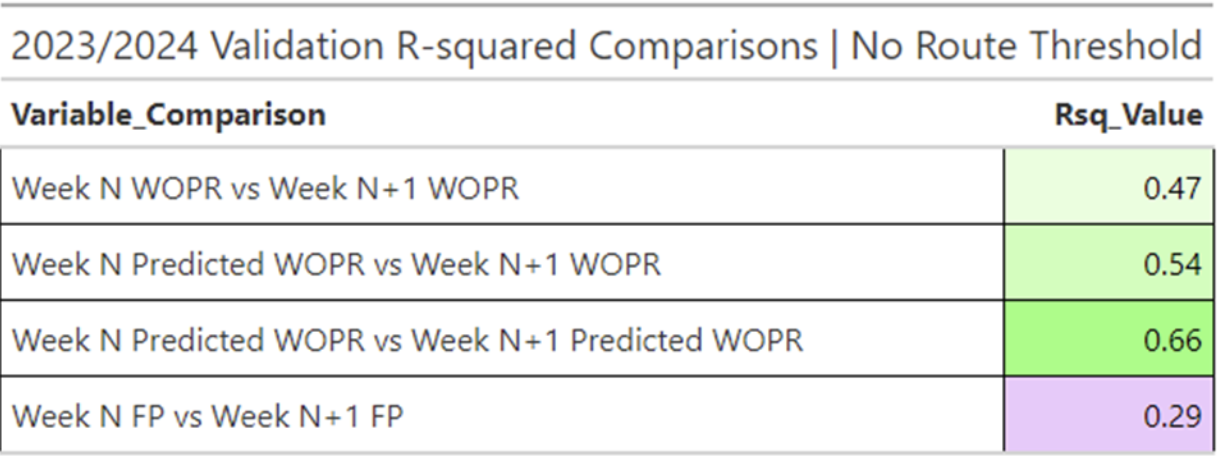
Before going into detail, I would like readers to know that predicted WOPR has the potential to outperform actual WOPR when it comes to predicting future performance. WOPR is widely considered one of the most consistent metrics in mainstream fantasy, with an R-squared (Rsq) of 0.47 when projecting N+1 WOPR for the 2023 season without any route threshold. In comparison, the predicted WOPR reaches 0.66 Rsq for forecasting N+1 predicted WOPR during the same season. This indicates a marked improvement in stability, with a raw increase in stability of Rsq of 0.19 compared to the best accepted acceptance rate available.

Additionally, the predicted WOPR appears to be more effective in predicting next week’s WOPR than the actual WOPR.

If you are interested in advanced fantasy football analysis, DFS or tail events, this article is for you.

Regression to the mean

Regression to the mean is a fundamental statistical concept that plays a critical role in predicting future performance, especially in the context of sports analytics. This refers to the tendency of extreme or outstanding performance to move closer to the mean (or mean) value when measured over time.

IN fantasy footballThis means that players who perform exceptionally well or poorly in a given week are likely to return to more typical levels of performance in the future.

For example, if a receiver has an unusually high target share or air yards share in one week, his performance will likely deteriorate in subsequent weeks, approaching normal levels. This is not to say that there can’t be outstanding results, but that outliers are often influenced by random factors that are not consistent from week to week, such as game script, defensive matchups, or even just luck.

In the context of WOPR, regression to the mean is an important principle because opportunity (or predicted opportunity in the case of my model) is inherently more stable than fantasy points (FP). While FP can fluctuate wildly based on touchdowns or big plays that may not always occur, WOPR measures a player’s ability on the field, which tends to remain more consistent over time.

Because WOPR is stable, we can use it to identify situations in which a player’s ability remains high, but his fantasy points are low due to short-term variance or bad luck.

This is where regression to the mean works in our favor: when we see a stable WOPR but low FP, it often signals an upcoming “explosive” game in which a player’s FP will likely catch up to the underlying opportunity they were getting. This gives us a forecasting edge, allowing us to anticipate breakthroughs before they happen.

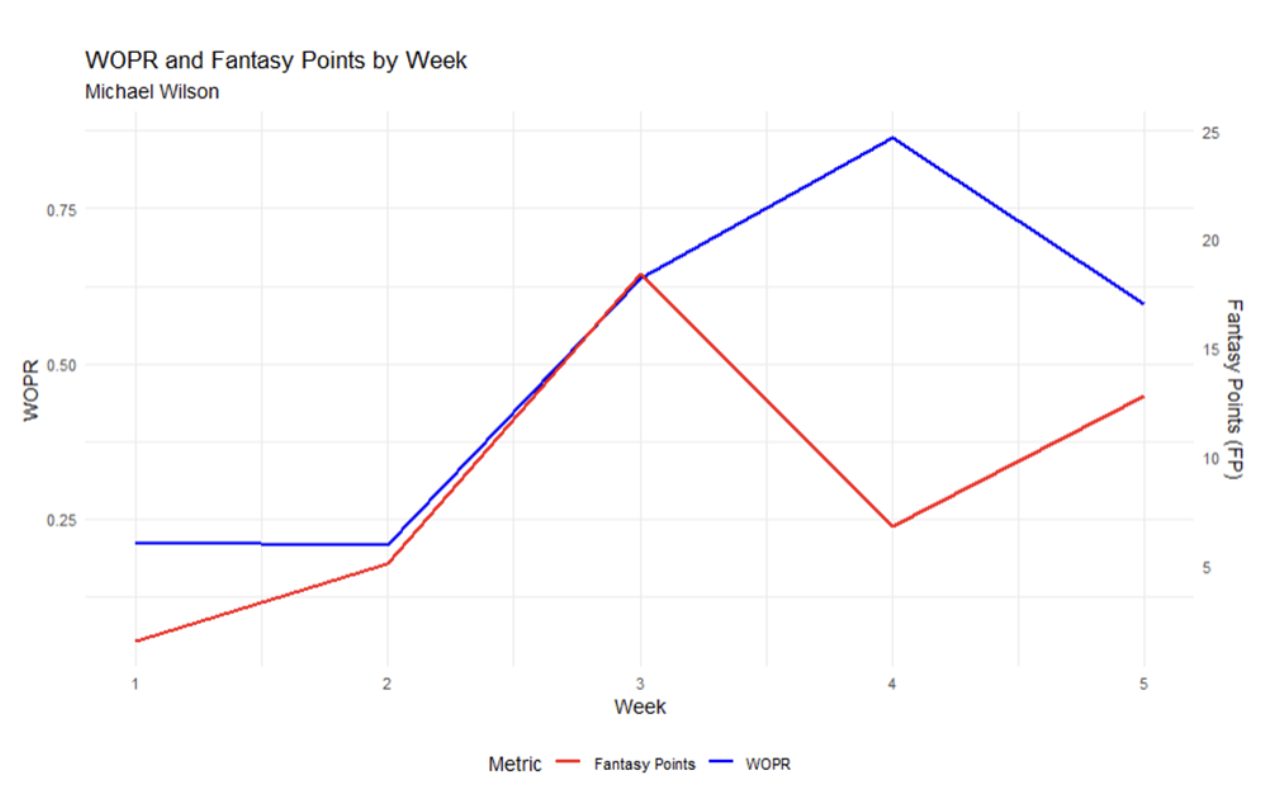
Here’s a good example of some regression to the mean for Michael Wilson.

In the chart, actual WOPR is shown in blue and Fantasy Points (FP) in red. In Week 4, we see Wilson’s actual WOPR spike to an impressive 0.86, but he didn’t take advantage of that opportunity, finishing with 6.8 fantasy points. While his WOPR remained high, it dropped to 0.59 the following week, but he scored more Fantasy Points (12.8).

We can use this effect to our advantage and model it accordingly.

Predicted WOPR is a better predictor of actual WOPR than actual WOPR itself. It is also more stable, making it an ideal candidate for creating a simple residual model.

Modeling predicted WOPR residuals

To create the predicted WOPR, we developed several complex models as described in my previous articles. However, the model we will use to predict fantasy points will be significantly less complex, but still effective. We only need simple linear regression. We aim to predict average 3-week fantasy scores using the 3-week predicted WOPR and then analyze the residuals.

Here are the regression results for the actual WOPR.

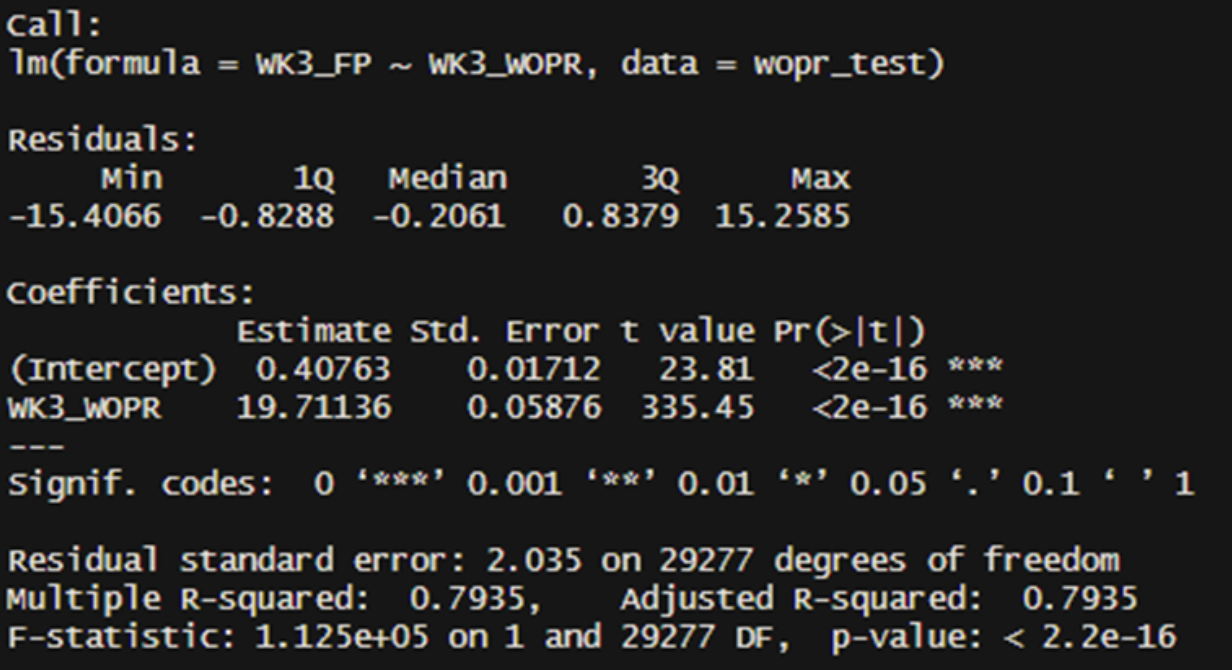
We see that our R-squared (Rsq) for predicting three-week fantasy points (per game) using three-week actual WOPR is 0.79. This means we can account for 79% of the variance in three-week fantasy points per game based on three-week actual WOPR.

This is a significant explanation of variance! This demonstrates that Actual WOPR effectively reflects what has happened over the past three weeks. However, it is important to note that we are not yet predicting future results.

Here are our regression results for the three-week forecasted WOPR.

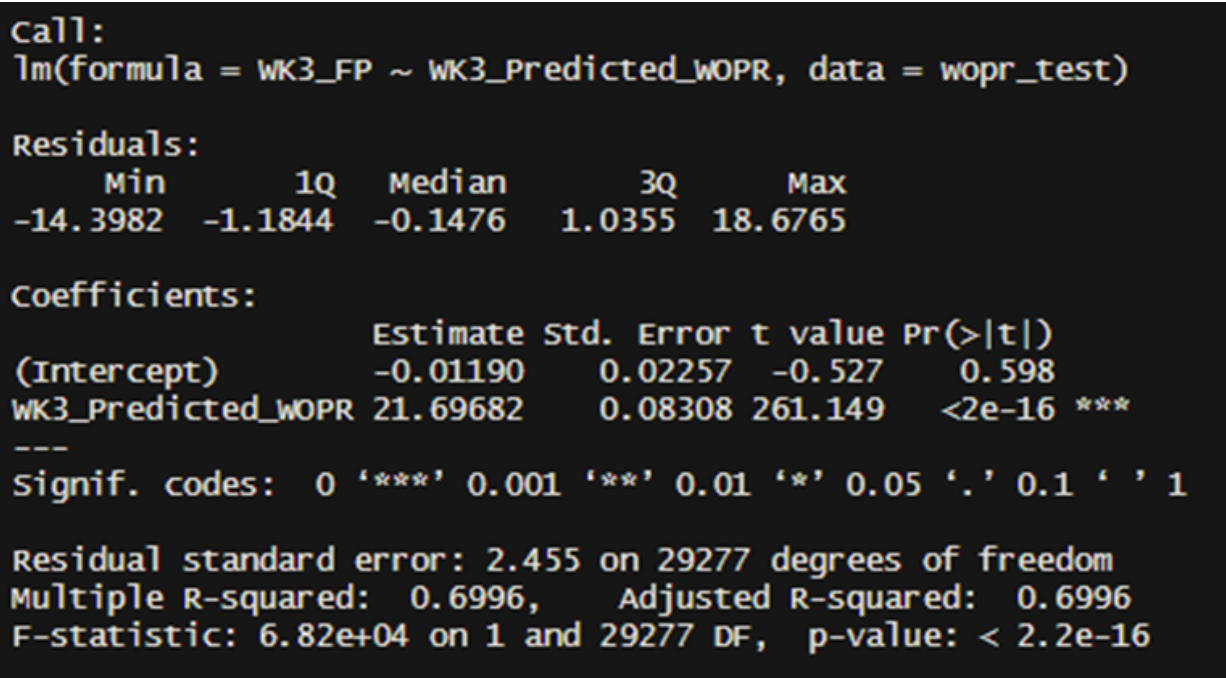
In the same context, our R-squared (Rsq) for the three-week predicted WOPR is 0.70, which is lower than the three-week actual WOPR.

This is understandable since actual WOPR reflects the opportunities that actually occurred, and fantasy points per game indicates the earnings from those opportunities. Remember, we are not predicting future results yet.

What ultimately matters is how the residuals predict future fantasy points. This is how we get an edge in fantasy, DFS, or any other analysis we do.

The residual represents the “error” of the model, or in other words, the variance that we cannot explain. Every forecast carries some degree of error. For example, if we predict that Zay Flowers will receive 10 targets and he only receives five, our residual will be -5. Conversely, if we predict AJ Brown will get 12 targets and he gets 15, our remainder will be 3.

This residual can serve as a powerful predictor for other models and variables when used effectively.

To use this effectively in Fantasy/DFS, we want to analyze the residuals of our three-week actual WOPR model and three-week predicted WOPR model to see how those residuals predict future results (next week). One of the important aspects we need to ensure our residual models do is that we somehow account for the performance of individual players.

Instead of simply predicting “Next week’s Fantasy Points”, I aim to predict “Next week’s Fantasy Points – 3-week FPpG”. This approach standardizes our response variable and helps us determine the true results of BOOM because it takes into account each player’s recent expectations.

For example, take Justin Jefferson, who averages 17 fantasy points per game (FPpG). If we project him to hit 19 FP next week, that would likely represent a high percentile projection in our model. However, this would not be a significant increase over the average for Jefferson.

Instead, we want to predict the difference between future and past averages. In this scenario, if we project Jefferson to have a modest 2 FP increase over his average, that would indicate a reliable forecast since he would only gain two FP above his average. This method allows us to better take into account the skills and situations of individual players. The main goal of this approach is to demonstrate that residuals can effectively help us predict player outliers.

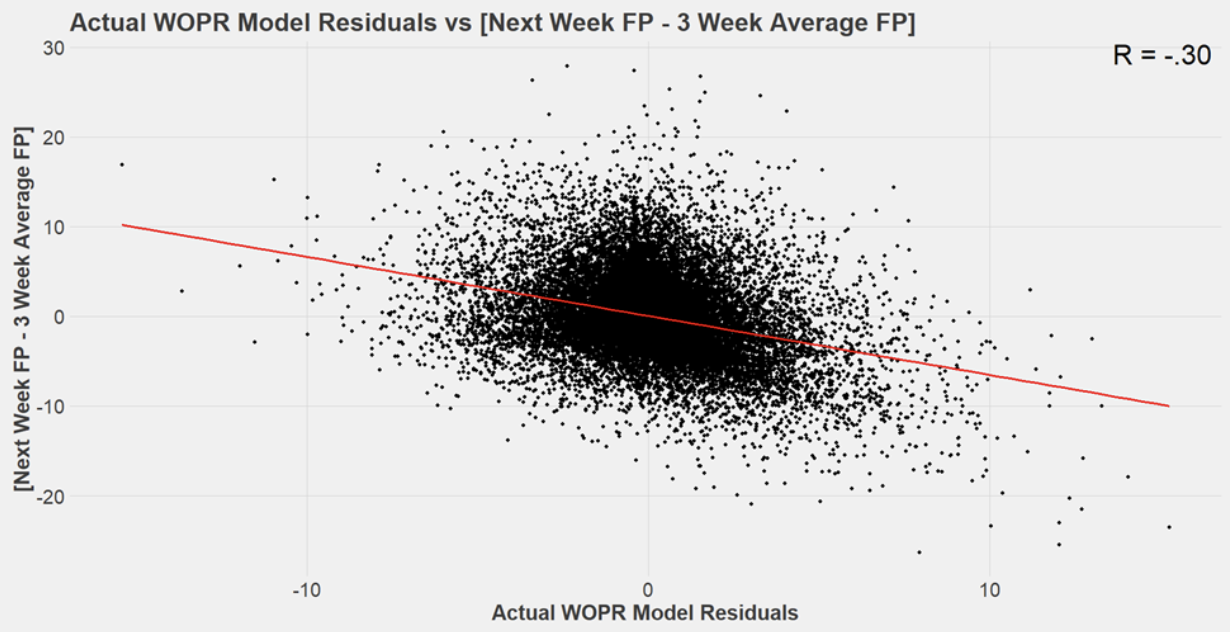
The graph above shows the residuals from our model of actual WOPR, showing a correlation of -0.3s (FP next week – FPpG at 3 weeks). This is a strong indication that our approach is effective for Actual WOPR.

In particular, it shows that players with a negative residual tend to exceed their expectations more often than players with a positive residual (regression to the mean).

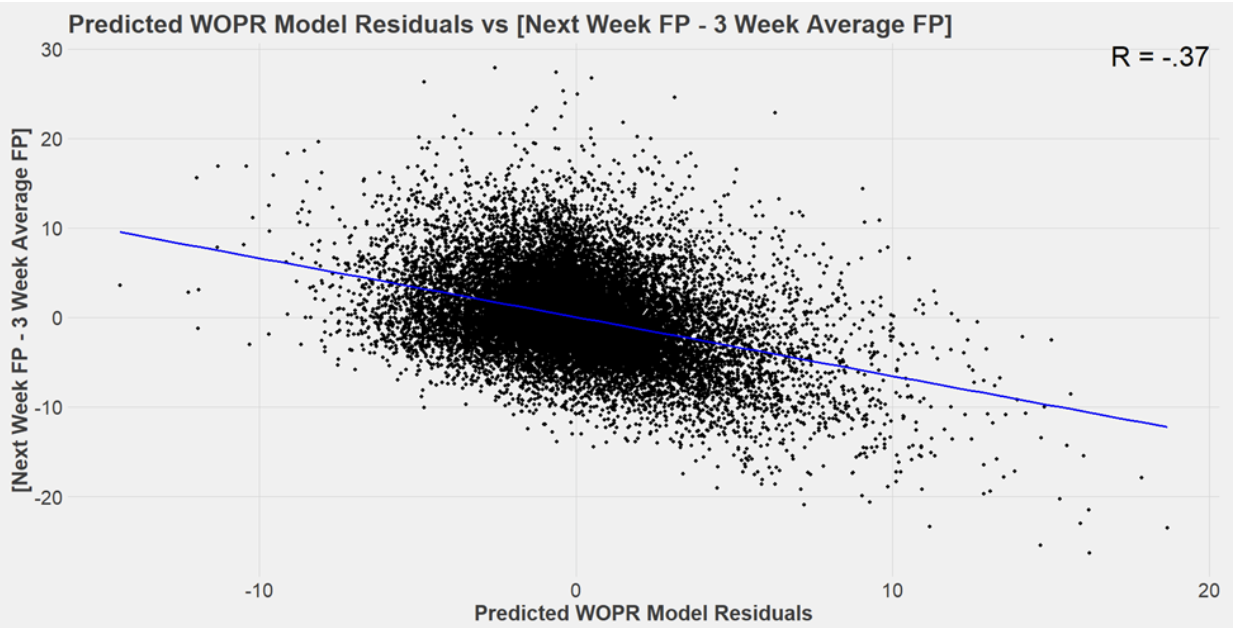
Here are the results for our predicted WOPR model residuals. As you can see, we improved the Pearson correlation by 0.07! This is promising news for our future success in fantasy. This 0.07 improvement in correlation means an increase in R-squared (Rsq) of 0.043. This means that our predicted WOPR model residuals can explain 4% more variance than the actual WOPR model residuals in (FP next week – FPpG at 3 weeks). Ultimately, this indicates that our predicted WOPR residuals are superior to the actual WOPR residuals, which are widely considered to be the best residual predictors in public use.

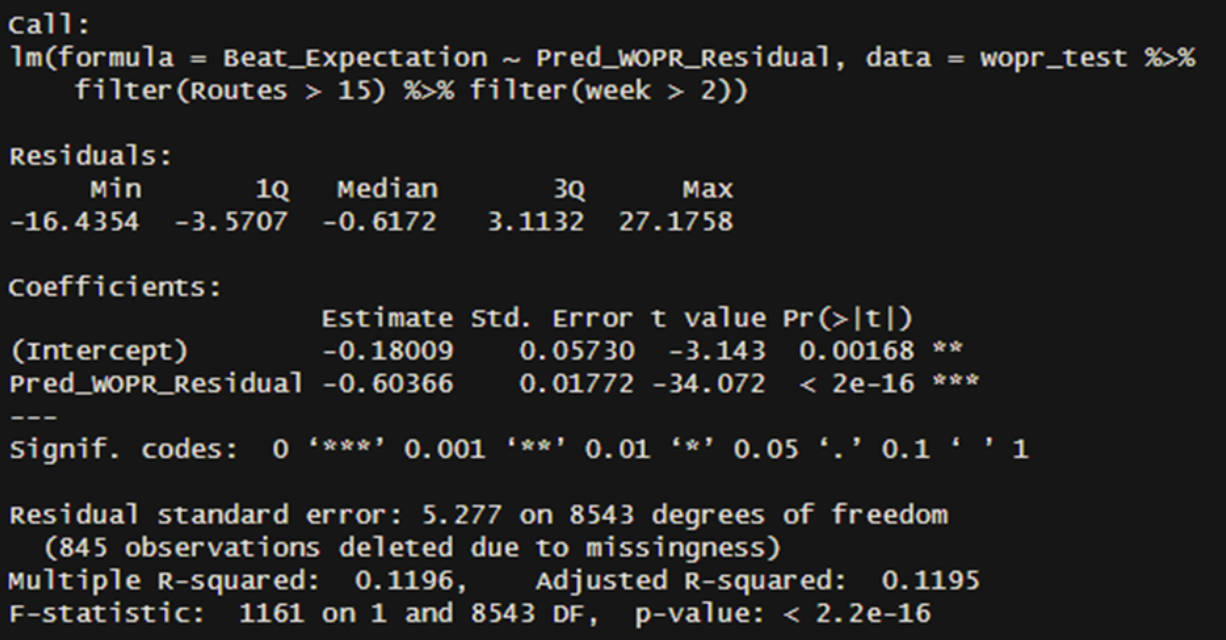
Using just our residuals, we can predict the expected excess (FP next week – FPpG for 3 weeks) with an R-squared (Rsq) of 0.12! This is a good result, especially since we are removing the three-week average fantasy score from our response variable. In comparison, the model using the actual WOPR produces an Rsq of 0.08, demonstrating that our predicted WOPR is better.

We can use this model to predict players’ performance from this week to the next.

Week 7: Route-Based Heroes

Players who are sometimes here to save the day!

“Route Based Heroes” is a weekly DFS/fantasy article I’d like to publish, looking at downside players in the three-week projected fantasy points model.

Remember that the residuals had a -0.37 correlation with each player’s fantasy beating in a given week. It was better than Actual WOPR.

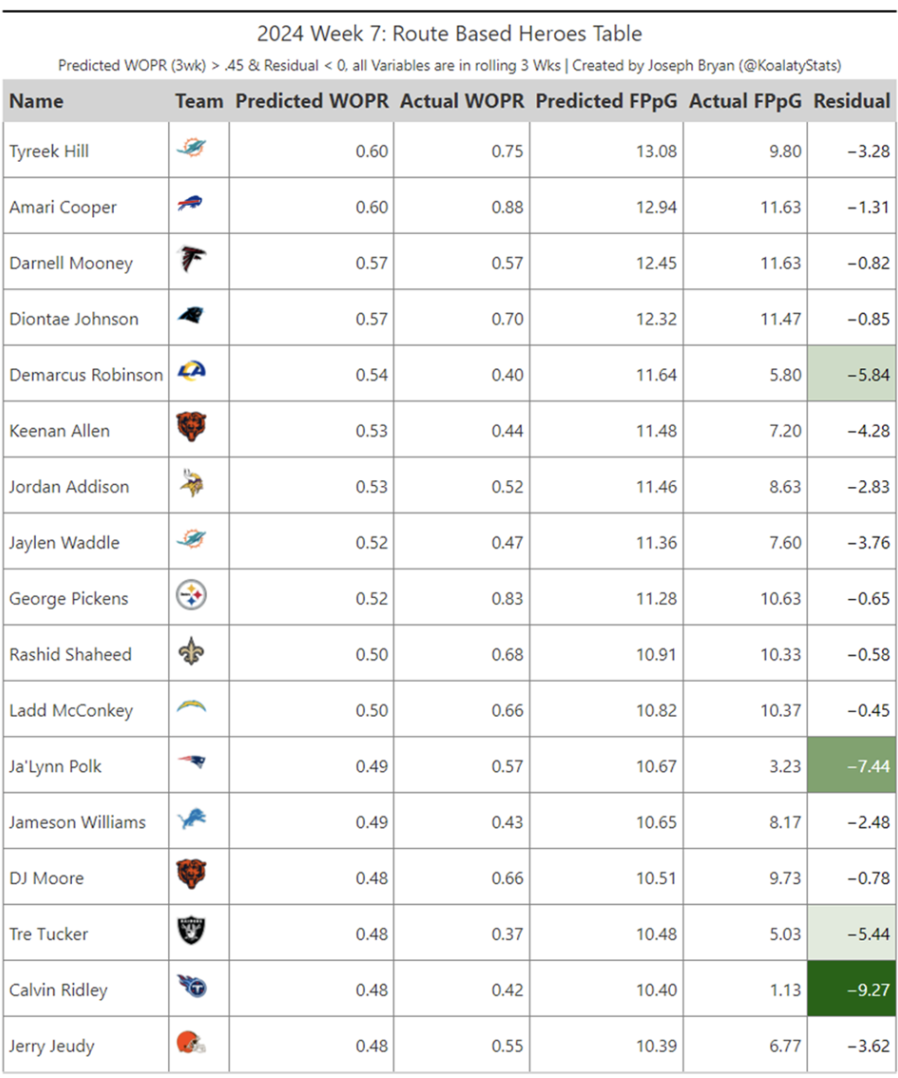
Here is a list of players with a high predicted WOPR and a model residual of less than 0.

Players with high projected WOPR run valuable routes and get open consistently. Players with a residual less than 0 need to perform better than expected to return to their average.

Think of this list as players who have a higher than average chance of success in the game.

• Calvin Ridley And Da’Lynn Polk stand out as candidates for super regression if their defenders can get the ball to them.

• With a new QB, Amari Cooper maybe we are in for a day of big positive regression. Judging by his routes and usage, he needs it.

• WITH Davante Adams outside the city, Tre Tucker you can see a surge in usage. He needs positive regression.

Any player on this list has a chance to achieve exceptional results based on our model and residual projections.